HP Prime benchmark
Err, right. The HP Prime is hardly a vintage calculator given that it was first released in 2015. Better still, HP released the so-called Prime "G2" in August 2018 with faster hardware, much more RAM to work with and double the storage space in flash memory.
When that happened, there was no excuse, I had to get one. At the time of writing, the Prime G2 would appear to be available only in Europe. The Americas have been left by the wayside this time around. I bought mine from derekenwinkel.nl with whom I have no affiliation other than being a happy customer of theirs.
As it became known that there was an updated version of the Prime, people in the Museum of HP Calculators Forum were interested in hard data showing the improvements in performance, so I went and wrote a benchmark.
The benchmark in itself is probably of limited value in absolute terms but gives a good idea of the differences between different machines.
A benchmark run can comprise up to three different types of test.
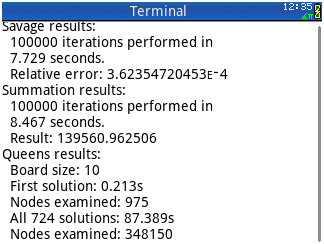
Firstly, there's the "Savage" test, which gives an idea of the accuracy of the calculator.
You start off with the value '1' in a variable. Let's say 'x' for argument's sake. You then calculate repeatedly:
\[ x = tan(atan(e^{ln(\sqrt{x^2})})) + 1 \]
If the calculator was absolutely accurate, this would be exactly the same thing as: \( x = x + 1 \)
But it's not completely accurate. With each iteration, a small error is introduced, which gets compounded into the next iteration etc. At the end of the test, when all the iterations have been calculated, we calculate the difference between the final result obtained and the "perfect" result, then we divide this discrepancy by the perfect result, which gives us the relative error. We also time how long it takes the calculator to perform the test.
Secondly, there's a summation test, which is designed to find out how quickly the calculator can chew on a series of calculations involving transcendental functions. In this case, we calculate:
\[ \sum_{k=1}^n \sqrt[^3]{e^{sin(atan(k))}} \]
It's a function with no intrinsic value or meaning other than it gets the calculator to work on trigonometric and exponential functions.
Finally, there's an implementation of a solution to the "N Queens" problem. We time how long it takes for the Prime to find the first solution and all the solutions to this problem on an 8x8, 9x9 or 10x10 board.
The "Num" and "Num Setup" views are used in this app. The app starts on the "Num Setup" view, in which you tell the benchmark how many iterations of the first two tests you want to run and how large a board you want to use for the "N Queens" test. When you hit the [OK] soft button it goes straight to the "Num" view, where it performs the tests and gives you the results:
Additional views in the "View" menu are "Reset", which as its name suggests, resets the preferences you set up in the "Num Setup" view, and "Last results", which displays again the results of the last test run without going through with the test.
Two variables are exported by this app: bmOptions and bmResults. Both are lists of raw data. bmOptions contains the options you gave in the "Num Setup" view and "bmResults" contains the results of the tests.
Tests can be invoked from the Home screen or from another app by using the exported DoBenchmark() function and passing to it a list of the form:
{a, b, c}
...where a represents the number of iterations of the Savage test to perform, b that of the Summation test and c the size of the board for the "N Queens" test. These numbers are, for a and b:
1: Skip the test
2: 1000 iterations
3: 2000 iterations
4: 5000 iterations
5: 10000 iterations
6: 20000 iterations
7: 50000 iterations
8: 100000 iterations
You can supply numbers greater than 8 if you wish. They will follow the same progression as the numbers 2 to 8 above, so 9 means 200000, 10 means 500000 etc.
For c, the number is:
1: Skip the test
2: 8x8 board
3: 9x9 board
4: 10x10 board
You can use numbers greater than 4 for c if you wish. The general case is, the board will be a (c+6)x(c+6) board.
So, to run 20000 iterations of the Savage test, 10000 iterations of the Summation test and the "N Queens" problem on an 8x8 board from the Home screen:
DoBenchmark({6,5,2})
(Don't forget to qualify the function if you're calling it from a different app: Benchmark.DoBenchmark())
You should get a list back something like this:
{
{"Savage", {20000, 0.14, 1.2980065E-6}},
{"Summation", {10000, 0.078, 13955.8578444}},
{"Queens", {8, 0.009, 876, 0.156, 92, 15720}}
}
This is a list of lists. Each list in this list contains two elements. The first is a string representing the name of the test and the second is another list containing the results of the test.
The meanings of the values within the result list depend on the test itself.
For the Savage test, the results are firstly the number of iterations performed, secondly the time in seconds taken to run the test, and thirdly the relative error.
For the Summation test, the first two elements of the result list are as for the Savage test, and the third element is the sum of the terms calculated during the course of the test.
For the "N Queens" test, the results are the size of the board, the time in seconds taken to find the first solution, the number of combinations examined to find that first solution, the time in seconds taken to find all of the solutions, the number of solutions found and, finally, the number of combinations examined to find all of the solutions.
An individual test's result is {0} if the test is not performed, so:
DoBenchmark({1,1,2})
Should give you something like this in return:
{
{"Savage", {0}},
{"Summation": {0}},
{"Queens", {8, 0.009, 876, 0.156, 92, 15720}}
}
All three tests show that the G2 is approximately three times as fast as its predecessor. The test results below are firstly from my Rev. C hardware Prime and then from my G2 below it.
You can download the benchmark app from here: Benchmark.hpappdir.zip